What is Single Layer Perceptron:

A Single layer perceptron is a type of neuron having multiple inputs and one output. Input has many dimensions i.e input can be a vector for example input x = ( I1, I2, .., In). Input nodes are connected to a node in the next layer. The node in the next layer takes the weighted sum of all its inputs.

for example input x = ( I1, I2, I3) = ( 5, 3.2, 0.1 )

\[Summedinput = 5 w_1 + 3.2 w_2 + 0.1w_3 \]

The output node having a threshold t. If summed input ≥ threshold, then it outputs y = 1 else it output y = 0.

The single layer perceptron does not have a previous knowledge, therefore the initial weights are assign randomly. SLP adds all of the weighted inputs and if the addition is above the threshold (any predetermined value), SLP is known to be in the activated state i.e output=1.

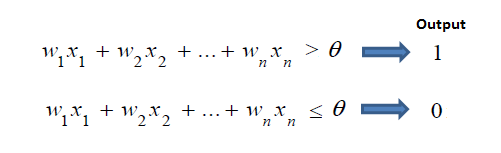
The perceptron receives the input values and does calculations to find the predicted output. If the predicted output is the same as that of the expected output, then the performance is considered satisfactory and no changes to the weights are made. But, if the predicted output does not match the expected output, then the weights need to be adjusted to reduce the error.

The algorithm is

• Initially, assigning all the weights to some random values

• Repeating (for many epochs):

1. Feed the network with an input from one of the examples in the training set

2. Compute the error between the output of the network and the desired output

3. Correct the error by adjusting the weights of the nodes

• Until the error is very small

]

A single layer percepron is simplest form of network to solve a problem with step or linear activation functions.

Single Layer Perceptron for XNOR problem in R

library(neuralnet)
XOR <- c(0,1,1,0)
xor.data <- data.frame(expand.grid(c(0,1), c(0,1)), XOR)
print(xor.data)
print(net.xor <- neuralnet(XOR~Var1+Var2, xor.data, hidden=0, rep=5))
plot(net.xor, rep="best")
round(predict(net.xor, data.frame(xor.data)))

Implementing Single Layer Perceptron for XNOR problem in Python

import numpy as np
from keras.models import Sequential
from keras.layers.core import Dense

We import numpy and alias it as np

Keras offers two different APIs to construct a model: a functional and a sequential one. We’re using the sequential API hence the second import of Sequential from keras.models.

Neural networks consist of different layers where input data flows through and gets transformed on its way. There are a bunch of different layer types available in Keras. These different types of layer help us to model individual kinds of neural nets for various machine learning tasks. In our specific case the Dense layer is what we want.

# the four different states of the XOR gate
training_data = np.array([[0,0],[0,1],[1,0],[1,1]], "float32")

# the four expected results in the same order
target_data = np.array([[0],[1],[1],[0]], "float32")

We initialize training_data as a two-dimensional array (an array of arrays) where each of the inner arrays has exactly two items.

We setup target_data as another two-dimensional array. All the inner arrays in target_data contain just a single item though. Each inner array of training_data relates to its counterpart in target_data.

model = Sequential()
model.add(Dense(1, input_dim=2, activation='sigmoid'))

Sets up an empty model using the Sequential API. Add a Dense layer to our model in which We set input_dim=2 because each of our input samples is an array of length 2 ([0, 1], [1, 0] etc.). 1 stand the dimension of the output for this layer. Our model means that we have two input neurons (input_dim=2) spreading into 1 neuron in output layer without any hidden layer as we are trying to mimic a single layer perceptron.

model.compile(loss='mean_squared_error',
              optimizer='adam',
              metrics=['binary_accuracy'])

]

With neural nets we always want to calculate a number (loss) that tells us how bad our model performs and then try to get that number lower. Mean_squared_error works as our loss function simply because it’s a well proven loss function. Then adam optimizer is usded to find the right adjustments for the weights. Last parameter metrics is the binary_accuracy which gives us access to a number that tells us exactly how accurate our predictions are.

model.fit(training_data, target_data, nb_epoch=500, verbose=2)

We kick off the training by calling model.fit(…) which require first two params, which are training and target data, the third one is the number of epochs (learning iterations), the last one tells keras how much info to print out during the training.

print(model.predict(training_data).round())

Using model.predict we can do predictions.

Summary:

McCulloch-Pitts neurons networks are computational devices, which are capable of performing any logical function. Single-Layer Perceptrons with step activation functions are constrained in what they can do. Adding additional hidden layers to the network will make it more powerful such that even non-linear relations can be predicted using such a neural network.